Unitary Matrix Networks in the Frequency domain¶

Imports¶

[1]:

# standard library
from collections import OrderedDict

# photontorch
import torch
import photontorch as pt

# other
import numpy as np
import matplotlib.pyplot as plt
from tqdm.notebook import trange

Settings¶

[2]:

%matplotlib inline
DEVICE = 'cpu'
np.random.seed(0)
torch.manual_seed(0)
np.set_printoptions(precision=2, suppress=True)
env = pt.Environment(freqdomain=True, num_t=1, grad=True)
pt.set_environment(env);
pt.current_environment()

[2]:

key	value	description
name	env	name of the environment
t	0.000e+00	[s] full 1D time array.
t0	0.000e+00	[s] starting time of the simulation.
t1	None	[s] ending time of the simulation.
num_t	1	number of timesteps in the simulation.
dt	None	[s] timestep of the simulation
samplerate	None	[1/s] samplerate of the simulation.
bitrate	None	[1/s] bitrate of the signal.
bitlength	None	[s] bitlength of the signal.
wl	1.550e-06	[m] full 1D wavelength array.
wl0	1.550e-06	[m] start of wavelength range.
wl1	None	[m] end of wavelength range.
num_wl	1	number of independent wavelengths in the simulation
dwl	None	[m] wavelength step sizebetween wl0 and wl1.
f	1.934e+14	[1/s] full 1D frequency array.
f0	1.934e+14	[1/s] start of frequency range.
f1	None	[1/s] end of frequency range.
num_f	1	number of independent frequencies in the simulation
df	None	[1/s] frequency step between f0 and f1.
c	2.998e+08	[m/s] speed of light used during simulations.
freqdomain	True	only do frequency domain calculations.
grad	True	track gradients during the simulation

Unitary Matrices¶

A unitary matrix is a matrix \(U\) for which \begin{align*} U\cdot U^\dagger = U^\dagger \cdot U = I \end{align*}

A unitary matrix is easily implemented in photonics. Indeed, according to the paper “`Experimental Realization of Any Discrete Unitary Matrix <https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.73.58>`__” by Reck et. al., Any unitary matrix can be written as a combination of phase shifters and directional couplers with variable coupling (or MZI’s) (Figure (a))

However, there exists an alternative approach to achieve any unitary operation, first proposed by Clements et. al. : Optimal design for universal multiport interferometers (Figure (b))

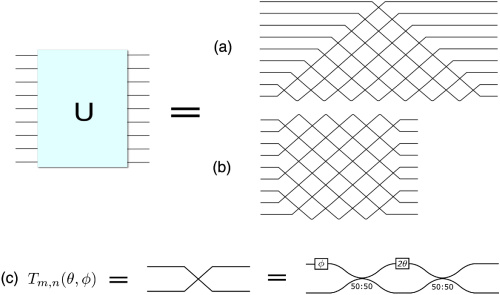
Unitary Matrix Paper

2x2 Unitary matrix (Reck)¶

Functions¶

[3]:

def array(tensor):
    arr = tensor.data.cpu().numpy()
    if arr.shape[0] == 2:
        arr = arr[0] + 1j * arr[1]
    return arr

def tensor(array):
    if array.dtype == np.complex64 or array.dtype == np.complex128:
        array = np.stack([np.real(array), np.imag(array)])
    return torch.tensor(array, dtype=torch.get_default_dtype(), device=DEVICE)

def rand_phase():
    return float(2*np.pi*np.random.rand())

class Network(pt.Network):
    def _handle_source(self, matrix, **kwargs):
        expanded_matrix = matrix[:,None,None,:,:]
        a,b,c,d,e = expanded_matrix.shape
        expanded_matrix = torch.cat([
            expanded_matrix,
            torch.zeros((a,b,c,self.num_mc-d,e), device=expanded_matrix.device),
        ], -2)
        return expanded_matrix
    def forward(self, matrix):
        ''' matrix shape = (2, num_sources, num_sources)'''
        result = super(Network, self).forward(matrix, power=False)
        return result[:,0,0,:,:]
    def count_params(self):
        num_params = 0
        for p in self.parameters():
            num_params += int(np.prod(p.shape))
        return num_params

def unitary_matrix(m,n):
    real_part = np.random.rand(m,n)
    imag_part = np.random.rand(m,n)
    complex_matrix = real_part + 1j*imag_part
    if m >= n:
        unitary_matrix, _, _ = np.linalg.svd(complex_matrix, full_matrices = False)
    else:
        _, _, unitary_matrix = np.linalg.svd(complex_matrix, full_matrices = False)
    return unitary_matrix

Define Network¶

[4]:

class Network2x2(Network):
    def __init__(self):
        super(Network2x2, self).__init__()
        self.s1 = pt.Source()
        self.s2 = pt.Source()
        self.d1 = pt.Detector()
        self.d2 = pt.Detector()
        self.mzi = pt.Mzi(length=0, phi=rand_phase(), theta=rand_phase(), trainable=True)
        self.wg1 = pt.Waveguide(length=0, phase=rand_phase(), trainable=True)
        self.wg2 = pt.Waveguide(length=0, phase=rand_phase(), trainable=True)
        self.link('s1:0', '0:mzi:1', '0:wg1:1', '0:d1')
        self.link('s2:0', '3:mzi:2', '0:wg2:1', '0:d2')

nw2x2 = Network2x2().to(DEVICE).initialize()

Check unitarity¶

To see which unitary matrix the network represents, we search for the result of the propagation of an identity matrix through the network. The power flag was set to false, as we are interested in the full complex output of the system. To show that this matrix is indeed unitary, we multiply with its conjugate transpose:

[5]:

def check_unitarity(nw):
    matrix = tensor(np.eye(nw.num_sources) + 0j)
    result = array(nw(matrix))
    print(result@result.T.conj())

check_unitarity(nw2x2)

[[1.+0.j 0.+0.j]
 [0.+0.j 1.-0.j]]

Check Universality¶

However, it would be more interesting if we can show that this network can act like any unitary matrix. We will now train the network to be equal to another unitary matrix by using the unitary property \(U\cdot U^\dagger=I\): we will train the network to obtain \(I\) with \(U_0^\dagger\) as input.

[6]:

def check_universality(nw, num_epochs=500, lr=0.1):
    matrix_to_approximate = unitary_matrix(nw.num_sources, nw.num_sources)
    matrix_input = tensor(matrix_to_approximate.T.conj().copy())
    eye = tensor(np.eye(nw.num_sources) + 0j)
    optimizer = torch.optim.Adam(nw.parameters(), lr=lr)
    lossfunc = torch.nn.MSELoss()
    epochs = trange(num_epochs)
    for i in epochs:
        optimizer.zero_grad()
        result = nw(matrix_input)
        loss = lossfunc(result, eye)
        loss.backward()
        optimizer.step()
        epochs.set_postfix(loss=f'{loss.item():.7f}')
        if loss.item() < 1e-6:
            break

    matrix_approximated = array(nw(eye))
    print(matrix_approximated)
    print(matrix_to_approximate)

[7]:

check_universality(nw2x2)


[[-0.29-0.62j  0.18+0.71j]
 [-0.34-0.65j -0.2 -0.65j]]
[[-0.29-0.62j  0.18+0.71j]
 [-0.34-0.65j -0.2 -0.65j]]

3x3 Unitary Matrix (Reck)¶

[8]:

class Reck3x3(Network):
    def __init__(self):
        super(Reck3x3, self).__init__()
        self.s1 = pt.Source()
        self.s2 = pt.Source()
        self.s3 = pt.Source()
        self.d1 = pt.Detector()
        self.d2 = pt.Detector()
        self.d3 = pt.Detector()
        self.mzi1 = pt.Mzi(length=0, phi=rand_phase(), theta=rand_phase(), trainable=True)
        self.mzi2 = pt.Mzi(length=0, phi=rand_phase(), theta=rand_phase(), trainable=True)
        self.mzi3 = pt.Mzi(length=0, phi=rand_phase(), theta=rand_phase(), trainable=True)
        self.wg1 = pt.Waveguide(length=0, phase=rand_phase(), trainable=True)
        self.wg2 = pt.Waveguide(length=0, phase=rand_phase(), trainable=True)
        self.wg3 = pt.Waveguide(length=0, phase=rand_phase(), trainable=True)
        self.link("s1:0",                         "0:mzi1:1",                        "0:d1")
        self.link("s2:0",             "0:mzi2:1", "3:mzi1:2", "0:mzi3:1",            "0:d2")
        self.link("s3:0", "0:wg1:1",  "3:mzi2:2", "0:wg2:1",  "3:mzi3:2", "0:wg3:1", "0:d3")
reck3x3 = Reck3x3().to(DEVICE).initialize()

Check Unitarity¶

[9]:

check_unitarity(reck3x3)

[[ 1.-0.j -0.+0.j  0.+0.j]
 [-0.+0.j  1.+0.j -0.+0.j]
 [ 0.+0.j -0.-0.j  1.-0.j]]

Check Universality¶

[10]:

check_universality(reck3x3)


[[-0.56-0.24j  0.13-0.51j  0.41-0.43j]
 [-0.25-0.25j -0.59+0.6j   0.4 -0.07j]
 [-0.56-0.44j  0.03+0.06j -0.62+0.32j]]
[[-0.56-0.24j  0.13-0.51j  0.41-0.43j]
 [-0.25-0.25j -0.59+0.6j   0.4 -0.07j]
 [-0.56-0.44j  0.03+0.06j -0.62+0.32j]]

3x3 Unitary Matrix (Clements)¶

[11]:

class Clements3x3(Network):
    def __init__(self):
        super(Clements3x3, self).__init__()
        self.s1 = pt.Source()
        self.s2 = pt.Source()
        self.s3 = pt.Source()
        self.d1 = pt.Detector()
        self.d2 = pt.Detector()
        self.d3 = pt.Detector()
        self.mzi1 = pt.Mzi(length=0, phi=rand_phase(), theta=rand_phase(), trainable=True)
        self.mzi2 = pt.Mzi(length=0, phi=rand_phase(), theta=rand_phase(), trainable=True)
        self.mzi3 = pt.Mzi(length=0, phi=rand_phase(), theta=rand_phase(), trainable=True)
        self.wg1 = pt.Waveguide(length=0, phase=rand_phase(), trainable=True)
        self.wg2 = pt.Waveguide(length=0, phase=rand_phase(), trainable=True)
        self.wg3 = pt.Waveguide(length=0, phase=rand_phase(), trainable=True)
        self.link("s1:0", "0:mzi1:1",             "0:mzi3:1", "0:wg1:1", "0:d1")
        self.link("s2:0", "3:mzi1:2", "0:mzi2:1", "3:mzi3:2", "0:wg2:1", "0:d2")
        self.link("s3:0",             "3:mzi2:2",             "0:wg3:1", "0:d3")
clem3x3 = Clements3x3().to(DEVICE).initialize()

Check Unitarity¶

[12]:

check_unitarity(clem3x3)

[[ 1.-0.j -0.+0.j -0.-0.j]
 [-0.+0.j  1.-0.j  0.+0.j]
 [-0.+0.j  0.-0.j  1.+0.j]]

Check Universality¶

[13]:

check_universality(clem3x3, num_epochs=1000)


[[-0.45-0.27j  0.05+0.52j  0.52+0.42j]
 [-0.64-0.35j  0.19-0.6j  -0.24+0.1j ]
 [-0.4 -0.16j -0.37+0.43j -0.33-0.62j]]
[[-0.45-0.27j  0.05+0.52j  0.52+0.42j]
 [-0.64-0.35j  0.19-0.6j  -0.24+0.1j ]
 [-0.4 -0.16j -0.37+0.43j -0.33-0.62j]]

NxN Unitary Matrix (Reck)¶

Creating those networks is quite cumbersome. However they are also implemented by photontorch, which then handles the creation of the networks:

[14]:

reck2x2 = pt.ReckNxN(N=2).to(DEVICE).terminate().initialize()
reck5x5 = pt.ReckNxN(N=5).to(DEVICE).terminate().initialize()
# quick monkeypatch to have the same behavior as the classes defined above
reck5x5.__class__ = Network

Check Unitarity¶

[15]:

check_unitarity(reck5x5)

[[ 1.+0.j -0.+0.j  0.+0.j -0.-0.j  0.+0.j]
 [-0.-0.j  1.+0.j  0.-0.j  0.+0.j  0.+0.j]
 [ 0.-0.j  0.+0.j  1.-0.j  0.+0.j -0.-0.j]
 [-0.+0.j  0.-0.j  0.-0.j  1.+0.j  0.+0.j]
 [ 0.-0.j  0.-0.j -0.+0.j  0.-0.j  1.+0.j]]

Check Universality¶

[16]:

check_universality(reck5x5)


[[-0.1 -0.4j  -0.15+0.52j -0.03+0.63j -0.01-0.06j  0.16+0.33j]
 [-0.28-0.28j -0.12+0.42j -0.09-0.57j  0.56-0.01j  0.02-0.05j]
 [-0.25-0.29j  0.24-0.54j -0.23-0.07j  0.11+0.21j  0.35+0.51j]
 [-0.24-0.4j  -0.02-0.4j   0.27+0.23j  0.26-0.37j -0.52-0.16j]
 [-0.28-0.47j -0.07+0.01j -0.24-0.16j -0.64+0.1j   0.04-0.43j]]
[[-0.1 -0.4j  -0.15+0.52j -0.03+0.63j -0.  -0.06j  0.16+0.33j]
 [-0.28-0.28j -0.12+0.42j -0.09-0.57j  0.56-0.01j  0.02-0.05j]
 [-0.25-0.29j  0.24-0.54j -0.23-0.07j  0.11+0.21j  0.35+0.51j]
 [-0.24-0.4j  -0.02-0.4j   0.27+0.23j  0.26-0.37j -0.52-0.16j]
 [-0.29-0.47j -0.07+0.01j -0.24-0.16j -0.64+0.1j   0.04-0.43j]]

NxN Unitary Matrix (Clements)¶

[17]:

clem5x5 = pt.ClementsNxN(N=5).to(DEVICE).terminate().initialize()
clem6x6 = pt.ClementsNxN(N=6).to(DEVICE).terminate().initialize()
# quick monkeypatch to have the same behavior as the classes defined above
clem5x5.__class__ = clem6x6.__class__ = Network

Check Unitarity¶

[18]:

check_unitarity(clem5x5)
check_unitarity(clem6x6)

[[ 1.+0.j  0.+0.j -0.-0.j -0.+0.j -0.-0.j]
 [ 0.-0.j  1.-0.j  0.-0.j  0.+0.j -0.-0.j]
 [-0.+0.j  0.+0.j  1.+0.j -0.+0.j  0.+0.j]
 [-0.-0.j  0.-0.j -0.+0.j  1.+0.j  0.+0.j]
 [-0.+0.j -0.+0.j  0.-0.j  0.-0.j  1.+0.j]]
[[ 1.+0.j  0.-0.j -0.+0.j  0.-0.j -0.+0.j -0.+0.j]
 [ 0.+0.j  1.-0.j  0.+0.j  0.+0.j -0.+0.j -0.+0.j]
 [-0.-0.j  0.-0.j  1.-0.j  0.-0.j -0.+0.j -0.-0.j]
 [ 0.+0.j  0.-0.j  0.+0.j  1.+0.j  0.-0.j  0.+0.j]
 [-0.-0.j -0.-0.j -0.-0.j  0.+0.j  1.+0.j -0.-0.j]
 [-0.-0.j -0.+0.j -0.+0.j  0.-0.j -0.+0.j  1.-0.j]]

Check Universality¶

[19]:

check_universality(clem5x5, num_epochs=1000)
check_universality(clem6x6, num_epochs=1000)


[[-0.21-0.33j  0.37+0.33j -0.41+0.21j  0.46+0.36j -0.03+0.23j]
 [-0.4 -0.33j -0.13+0.27j  0.21-0.15j  0.21-0.14j -0.1 -0.71j]
 [-0.34-0.33j -0.2 +0.15j  0.16+0.57j -0.54-0.06j -0.13+0.24j]
 [-0.28-0.41j -0.21-0.49j  0.16-0.44j  0.2 +0.04j -0.17+0.42j]
 [-0.15-0.29j  0.56-0.06j -0.18-0.36j -0.48-0.17j  0.39-0.06j]]
[[-0.21-0.32j  0.36+0.33j -0.41+0.22j  0.46+0.36j -0.03+0.23j]
 [-0.4 -0.33j -0.13+0.27j  0.21-0.15j  0.21-0.14j -0.1 -0.71j]
 [-0.34-0.33j -0.2 +0.15j  0.16+0.57j -0.54-0.06j -0.13+0.24j]
 [-0.28-0.42j -0.21-0.49j  0.16-0.43j  0.2 +0.04j -0.17+0.42j]
 [-0.15-0.29j  0.56-0.06j -0.19-0.35j -0.48-0.17j  0.39-0.06j]]


[[-0.19-0.48j -0.3 +0.26j  0.2 -0.31j -0.03+0.12j -0.12+0.6j   0.23-0.02j]
 [-0.31-0.25j -0.36-0.11j -0.23+0.33j  0.14+0.13j  0.05-0.41j  0.56-0.13j]
 [-0.37-0.3j  -0.18+0.13j -0.15+0.43j -0.13-0.03j -0.01+0.02j -0.62+0.33j]
 [-0.11-0.34j  0.09+0.24j  0.3 -0.41j -0.26-0.35j  0.08-0.59j -0.03+0.04j]
 [-0.2 -0.27j  0.5 -0.21j -0.04+0.11j  0.45-0.52j -0.23+0.16j  0.13+0.09j]
 [-0.15-0.28j  0.41-0.35j  0.44+0.16j -0.1 +0.5j   0.14-0.02j -0.12-0.29j]]
[[-0.19-0.48j -0.3 +0.26j  0.2 -0.31j -0.03+0.12j -0.12+0.6j   0.23-0.03j]
 [-0.31-0.25j -0.36-0.11j -0.23+0.33j  0.14+0.13j  0.06-0.41j  0.56-0.13j]
 [-0.37-0.3j  -0.18+0.13j -0.15+0.43j -0.13-0.03j -0.01+0.02j -0.62+0.33j]
 [-0.11-0.34j  0.09+0.24j  0.3 -0.41j -0.26-0.35j  0.08-0.59j -0.03+0.04j]
 [-0.21-0.27j  0.5 -0.21j -0.04+0.11j  0.45-0.52j -0.23+0.16j  0.13+0.09j]
 [-0.15-0.28j  0.41-0.35j  0.44+0.16j -0.1 +0.5j   0.14-0.02j -0.12-0.29j]]

Unitary Matrix Networks in the Frequency domain¶

Imports¶

Settings¶

Unitary Matrices¶

2x2 Unitary matrix (Reck)¶

Functions¶

Define Network¶

Check unitarity¶

Check Universality¶

3x3 Unitary Matrix (Reck)¶

Check Unitarity¶

Check Universality¶

3x3 Unitary Matrix (Clements)¶

Check Unitarity¶

Check Universality¶

NxN Unitary Matrix (Reck)¶

Check Unitarity¶

Check Universality¶

NxN Unitary Matrix (Clements)¶

Check Unitarity¶

Check Universality¶

Photontorch

Navigation

Related Topics